Je li Pi polinom?

Video: Je li Pi polinom?

2024 Autor: Lynn Donovan | [email protected]. Zadnja promjena: 2023-12-15 23:47

Pi (π) se ne smatra a polinom . To je vrijednost koja se odnosi na opseg kružnice. S druge strane, polinom odnosi se na jednadžbu koja sadrži četiri ili više varijable.

Može li pi biti dio polinoma?

Odgovor je NE. Ako je postojao a polinom s algebarskim koeficijentima, bilo bi i a polinom s racionalnim koeficijentom (s većim stupnjem). To je zato što je ˉQ algebarski zatvoren. Pretpostavljam da π bili su korijen a polinom f(x)=xn+an−1xn−1+⋯+a0 pri čemu su ai algebarski brojevi.

Drugo, što čini polinom? U matematici, a polinom je izraz koji se sastoji od varijabli (koji se također nazivaju neodređenim) i koeficijenata, koji uključuje samo operacije zbrajanja, oduzimanja, množenja i nenegativnih cjelobrojnih eksponenata varijabli. Primjer a polinom od jednog neodređenog, x, je x² − 4x + 7.

U tom smislu, je li Pi monom?

Da, π π je a monom jer je broj.

Mora li polinom imati varijablu?

Dakle: A polinom limenka imati konstante, varijable i eksponenti, ali nikada dijeljenje s a varijabla . Također mogu imati jedan ili više pojmova, ali ne i beskonačan broj pojmova.

Preporučeni:

Kako se zove polinom sa 6 članova?

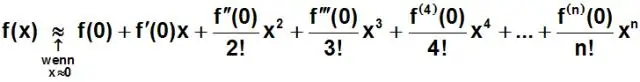
Sljedeći nazivi polinoma se dodjeljuju prema stupnju: 4. stupanj – kvartični (ili, ako svi pojmovi imaju paran stupanj, bikvadratični) 5. stupanj – kvintični. Stupanj 6 – sekstični (ili, rjeđe, heksički)

Što je polinom prvog stupnja?

Polinomi prvog stupnja. Polinomi prvog stupnja poznati su i kao linearni polinomi. Konkretno, polinomi prvog stupnja su linije koje nisu ni horizontalne ni okomite. Češće se slovo m koristi kao koeficijent od x umjesto a, a koristi se za predstavljanje nagiba linije